Benefits of the Cone Penetrometer Test
- Accurately profiles the geological strata
- Accurately predicts vertical pile capacity for deep foundations
- Measures the low strain shear wave velocity for seismic evaluations satisfying International Building Code (IBC) requirements
- Makes fair predictions of time rate of consolidation and permeability tests through pore pressure dissipation tests—good for wick drain design
- In normally consolidated or recently aged cohesionless soils, provides fair estimates of settlement for shallow foundations
In-Situ Soil Testing often performs CPT with the direct push truck that Dr. Schmertmann used for his pioneering research (Good Karma) [First direct push truck in North America—history]. To assure high quality control, a registered professional engineer performs the tests.
History of Cone Penetrometer Test (CPT), ASTM D 3441 and D 5778: The mechanical cone penetrometer probe, invented in The Netherlands in 1932 by P. Barentsen, measures the quasi-static thrust required to push a solid, conical tip having a 60 degree apex angle and a cross‑sectional area of 10 cm2 into the foundation soil. The operator advances the cone using a nested, dual‑rod system, the outer rods providing strength to penetrate the cone in a collapsed configuration, and the inner rods allowing him or her to advance only the cone tip at each test depth (generally at 20-cm intervals) while measuring the hydraulic thrust pressure at the top of the rods. In 1953, Begemann modified the probe to include a friction sleeve just behind the tip. For the friction cone test, the inner rods initially advance only the tip for a short distance, and then engage both the tip and a friction sleeve together. The unit soil adhesion acting on the center of the friction sleeve, located 20 cm above the tip, equals total thrust of the tip and friction sleeve minus the tip-only thrust force (from the previous test depth) and then divided by the sleeve area of 150 cm2. The engineer then divides the unit adhesion by the unit tip bearing from the previous test depth to determine the friction ratio (both readings then apply to the same depth). However, the term “friction” is a misnomer as it has no meaning to the shear strength of soil. Cohesionless soils that have higher shear strengths than cohesive soils have lower “friction ratios” than cohesive soils. Empirical charts identify the type of soil based on how it behaves either drained or undrained.
The improvement of electronics and computers in the 1980s led to the development of stainless-steel electrical cone penetrometer probes that obtain and record more reliable test measurements and eliminate the dual-rod system. Because the electric cones make measurements continuously instead of stopping every 20 cm as mechanical cones do, the electric cone soundings take slightly less time to perform than mechanical cone soundings. Strain gauges measure the tip and friction resistances and a pressure transducer measures the pore water pressures generated during penetration. With the electric cone, data are collected at penetration increments of 0.5 cm to 5 cm depending on the computer acquisition system (ours uses 1 cm) [Figure 1].
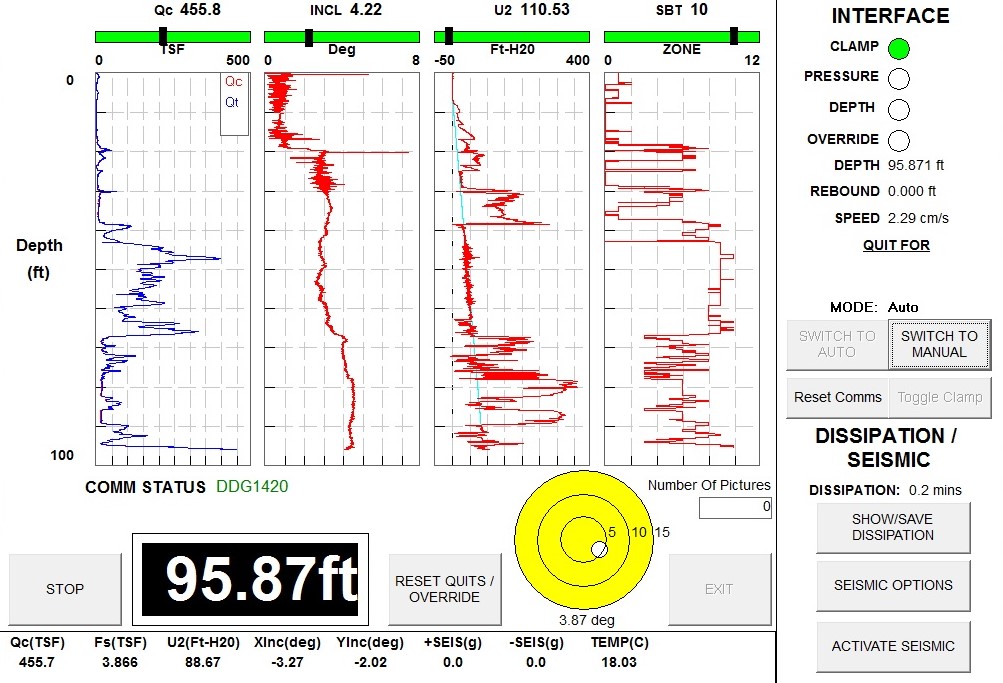
Figure 1: Screenshot of CPT data acquisition
Engineers prefer the electronic cone’s accuracy and productivity, relegating the mechanical cone to profiles containing strong materials that might damage the more expensive electrical cone. The cone penetrometer can penetrate soil with an N60-value of about 50 blows per foot with a 15 ton (13,000 kgf) direct push rig or soil with an N60-value of about 30 blows per foot with a 5 ton (4,000 kgf) heavy drill rig. The adapter that connects the cone to the push rods has a larger diameter than the push rods making a larger diameter hole and minimizing soil adhesion along the push rods (named a friction reducer).
By monitoring the inclination sensors, the engineer can follow the data collection computer screen’s graph of inclination versus depth as the CPT probe advances into the soil. Anomalies, such as cobbles, concrete or bricks, can cause the probe to deflect significantly. After disconnecting the depth recording cable, the engineer can cycle the probe up and down the sounding. Often, the probe will resume advancing more vertically. Sometimes, the probe can get a slight bend in it and after rotating the rods 180o, the sounding will straighten as the probe wants to go one direction and the push rods want to go the opposite direction.
CPTU Measurements
The electric CPT probe quasi-statically penetrates the soil at a constant 2 cm/sec rate measuring the tip, side friction, pore pressure, inclination, and temperature using calibrated strain gauges and transducers. The cone penetrometer probe digitally processes all measurements and then transmits them to the computer inside the push rig. Digitally processing the data downhole makes the measurements more accurate than its predecessor, analog processing systems that transmit voltages through a cable to a computer and then convert those voltages into measurements. When processing the CPT data, the engineer computes the vertical depth by correcting the push distance with the inclination measurements, using the following formula:
Dvert = Dpush * cosine (inclination),
Where Dvert = Vertical Depth
Dpush = Pushed Depth
Inclination expressed in radians
To eliminate all compressible air that would create inaccurate pore pressure measurements, the engineer must fully saturate the pore pressure transducer and filter. He/she fills the cavity between the tip and transducer with silicon oil, waits for all air bubbles to rise to the top, and screws on the tip that has a hole from its bottom to filter side (two connecting holes at 90 degrees) forcing the oil and any air to exit through the hole at the inside of the filter (Figures 2a-c).
Figures 2a-c: Saturating pore pressure transducer
When only oil exits, the engineer confirms a fully saturated pore pressure transducer system. The engineer should use polyethylene porous filters pre-saturated with silicon oil (preferably by the manufacturer). The rigidity of polyethylene prevents the filter from compressing which would cause pore pressure measurement error. Because pore pressures can occur behind the cone tip, the measured tip resistance, qc, is corrected to, qt, using the following formula:
qt = qc + u(1-a), where
qt = the corrected total tip resistance,
qc = the measured tip resistance,
u = pore pressure generated immediately behind the tip,
a = net area ratio
As shown on Figure 3, researchers have measured pore water pressures at 3 locations on the cone penetrometer: 1) on the face of the tip (U1 position), 2) behind the tip (U2 position), and 3) behind the friction sleeve (U3 position). U1 position filters always measure positive pressures but abrade from high stresses in granular soil. U2 position filters generally measure positive pressures and can measure negative pressures in highly over-consolidated soil. With U2 position pore pressure measurements, the engineer corrects the tip stresses for the pore pressure behind the tip as shown on the above equation and as a result prefers this location. Only researchers have used U3 position pore pressure measurements, and it has some difficulties becoming fully saturated. To minimize this pore pressure correction for the U2 position filter, cones should have high net area ratios (ours is 0.8) and this correction is generally less than 2%. Pore pressure can also affect friction measurements. Friction sleeve should have equal end areas at the front and back to eliminate those potential pore pressure corrections, which most cones now have.
Figure 3: Pore pressure filter locations
Figure 4 shows the start of a CPTU sounding with a 10 cm2 piezocone, friction reducer, rubber rod wiper to keep soil below and out of the truck work space, and lateral supporting guide tube to prevent rod buckling.
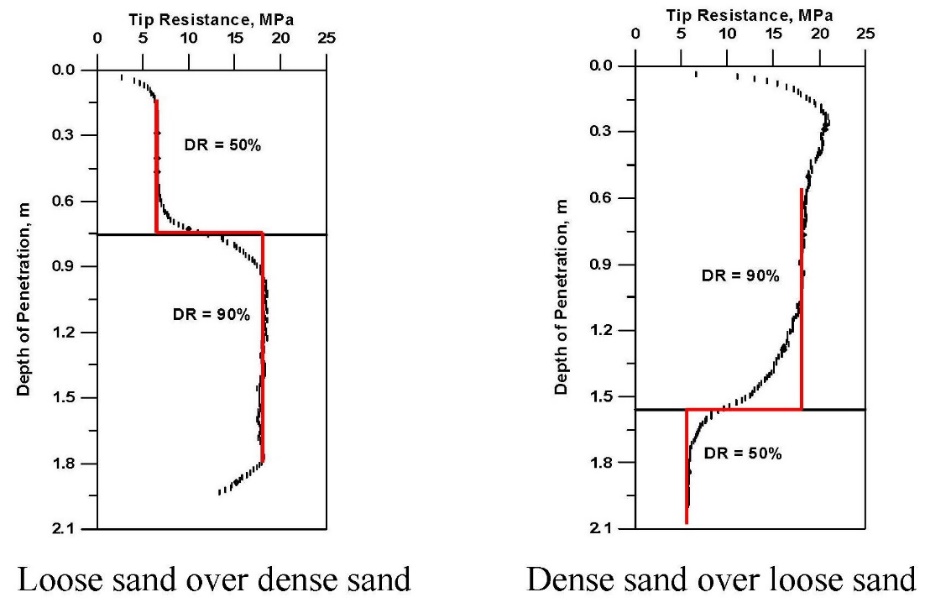
Smaller diameter cones create smaller stress bulbs than larger cones. As a result, smaller cones more accurately measure soil properties at boundaries of differing soil stiffnesses or strengths. 10 cm2 cones more accurately measure soil properties than 15 cm2 cone penetrometers. Ahmadi, Byrne and Campanella (1999) illustrate the importance of smaller projected area CPT probes on the below graphs–smaller stress bulbs more closely follow the correct red lines (Figure 5).
Figure 5: Shows the parasitic effect of larger stress bulbs from cones larger than 10 cm2
Seismic Measurements
The ASTM downhole seismic method requires an energy source to firmly contact the soil surface from a horizontally offset location and geophones mounted in the probe that can measure the generated shear waves. The energy source consists of a seismic plate and a hammer. Placing the seismic plate just below a leveling jack ensures good coupling between the plate and soil. Placing a rubber pad between the seismic plate and jack makes sure the energy travels into the soil rather than shake the push rig (Areias, Haegeman, Van Impe, 2004). When a sledge hammer, pendulum hammer or automatic hammer strikes the plate horizontally, the plate generates a shear wave with horizontal particle motion and vertical direction of propagation (Figure 6).
Figure 6: Horizontal strike to create seismic shear wave
A very accurate and repeatable trigger starts the elapsed time clock the instant that the hammer strikes the plate. The data acquisition computer that simulates an oscilloscope collects and stores the seismic shear wave after each strike. Most CPT systems have only one set of geophones in the probe. After measuring a seismic wave, the engineer must advance the seismic CPT probe and make another horizontal strike. Termed the psuedo-interval method defines this procedure that uses one set of geophones and two depths and sets of strikes/generated waves. He/she generally performs tests at one meter intervals because these intervals conveniently coincide with the end of a push stroke and pausing pushing to add another rod.
The engineer should use either the cross-over method or cross-correlation method to choose the arrival time for each horizontal shear wave (Sully and Campanella, 1995). With the cross-over method, the engineer chooses the time where the wave crosses zero amplitude after the first wave peak or valley. He/she chooses the same location for subsequent waves. The computer calculates the shear wave velocities (Vs) by dividing differences in the hypotenuse travel distances by the differences in arrival times for consecutive test depths. The engineer should check the calculated shear wave velocities to confirm that they make sense with the soil profile and tip resistances. Figure 7 shows an example of sets of seismic waves, where the engineer used the crossover method to find the arrival times. With the cross-correlation method, a computer mathematically shifts the wave at the lower test depth by a delta time until it superimposes on the shear wave at the higher depth. The cross-correlation method works best for measuring systems that have two sets of geophones vertically spaced apart at a constant distance in the probe or module above the probe and one strike creates both sets of waves, also known as the true interval measurement. The engineer can compute the low strain or maximum shear modulus using the following equation:
GMAX = ρ * Vs2
Where GMAX = low strain or maximum shear modulus
ρ = mass density of the soil
Vs = shear wave velocity
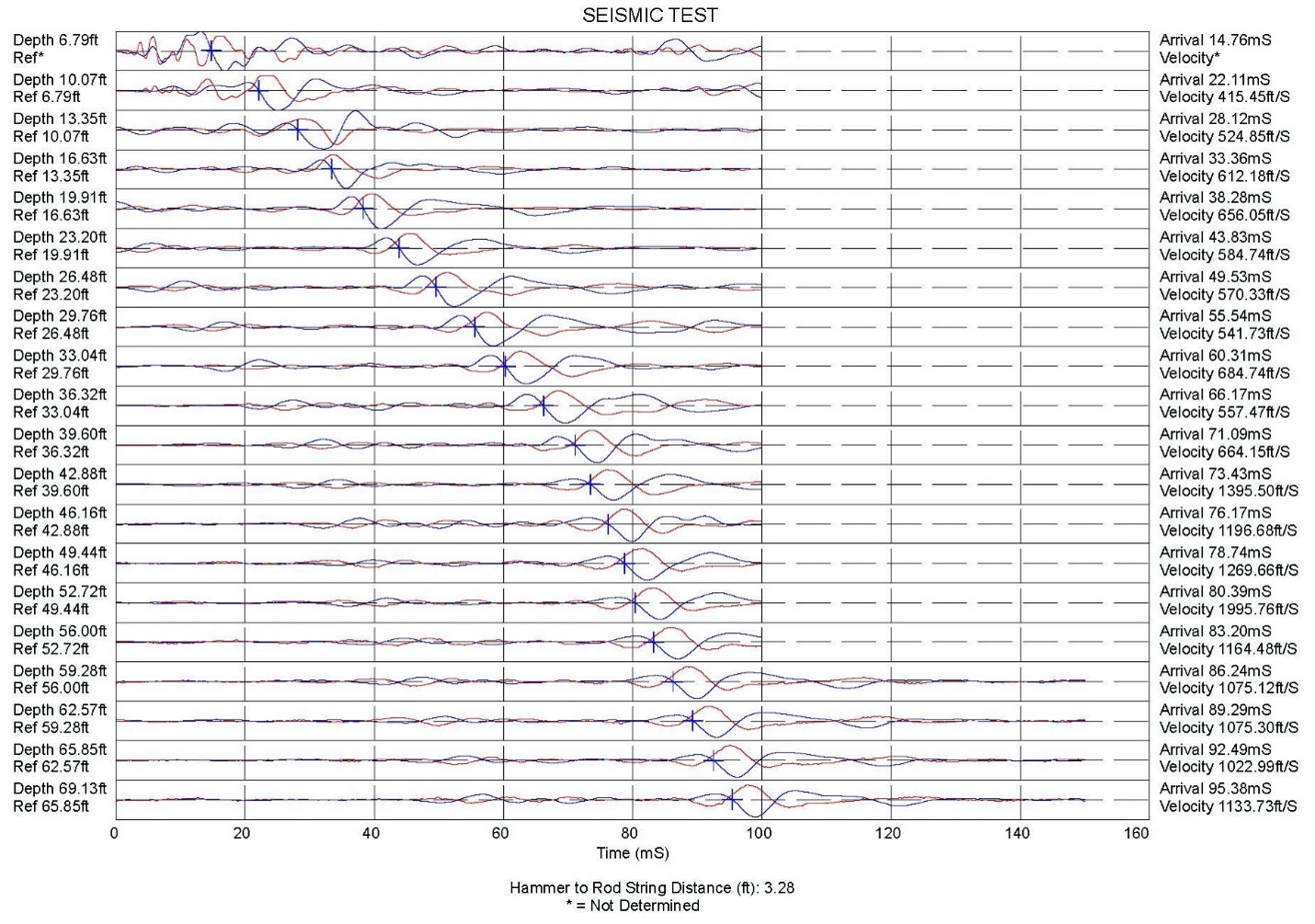
Figure 7: Example of seismic shear waves and choosing their arrival times with cross-over method
Pore Pressure Dissipation Tests
Ch = R2 T50/t50
kh = Ch γw/Mh where
Ch = time rate of consolidation in the horizontal direction
R = the radius of the CPT tip
R2 = 0.000318 m2 for a 10 cm2 cone
T50=time factor for 50% dissipation from the below family of curves(Battaglio,et.al.,1981)[Figure9]
t50 = time for 50% of dissipation to occur
kh = horizontal coefficient of permeability
γw = unit weight of water
Mh = constrained deformation modulus in the horizontal direction
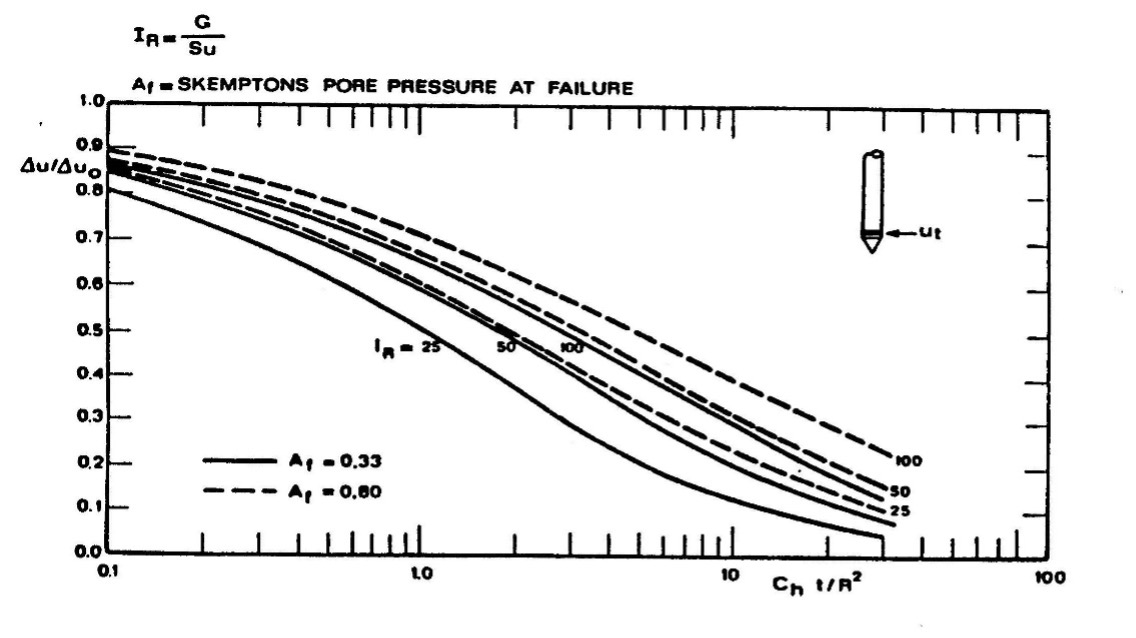
Figure 9: Family of dissipation test curves
Af approximates 0.8 for soft clay, while Af approximates 0.33 for stiff clay. Krage, et. al., 2014 suggests computing the rigidity index, IR using the below formula.
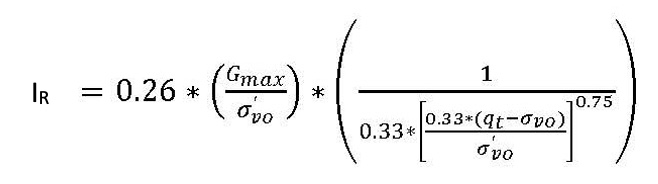
Where IR = rigidity index
GMAX = low strain shear modulus
σ’vo = effective vertical stress
σvo = total vertical stress
qT = corrected tip resistance
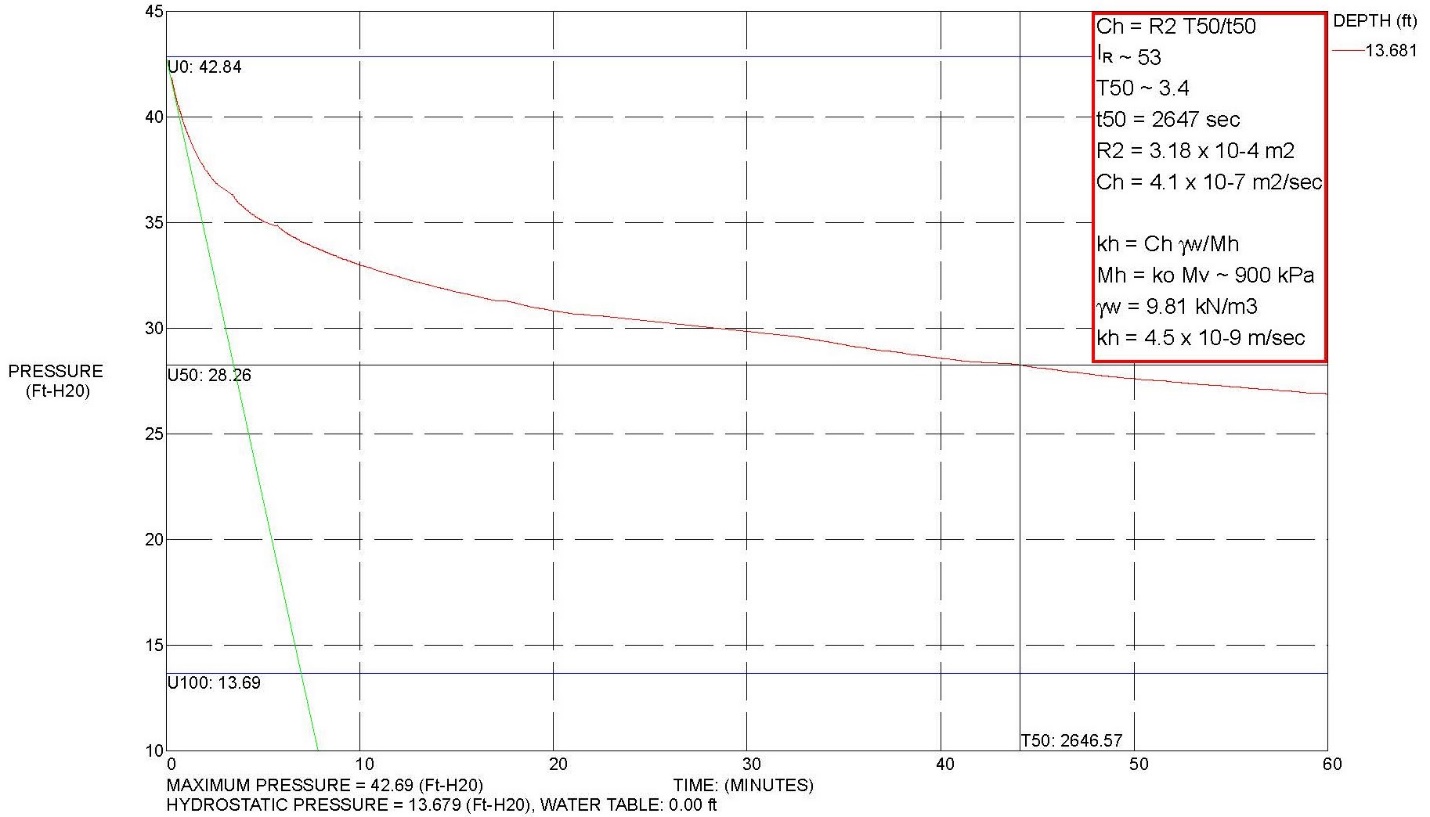
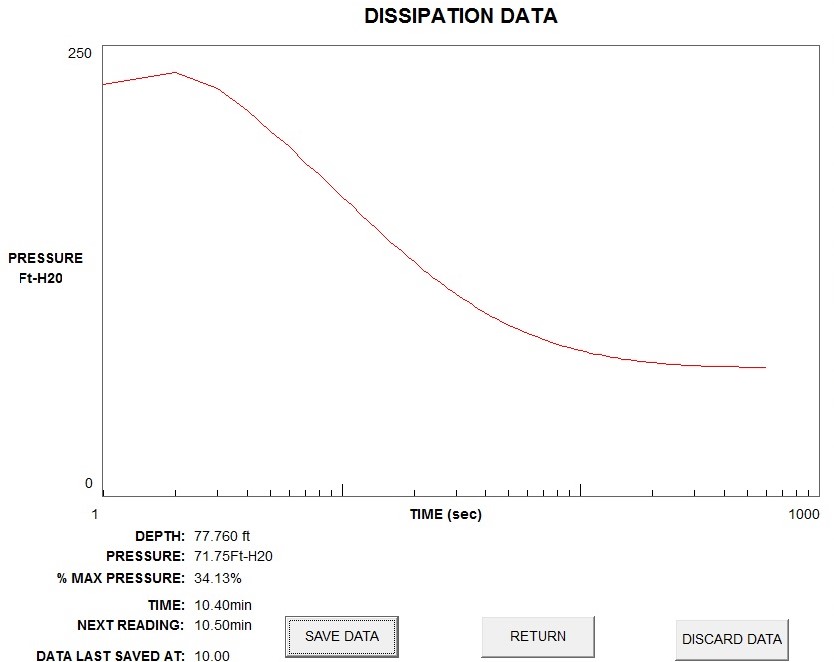
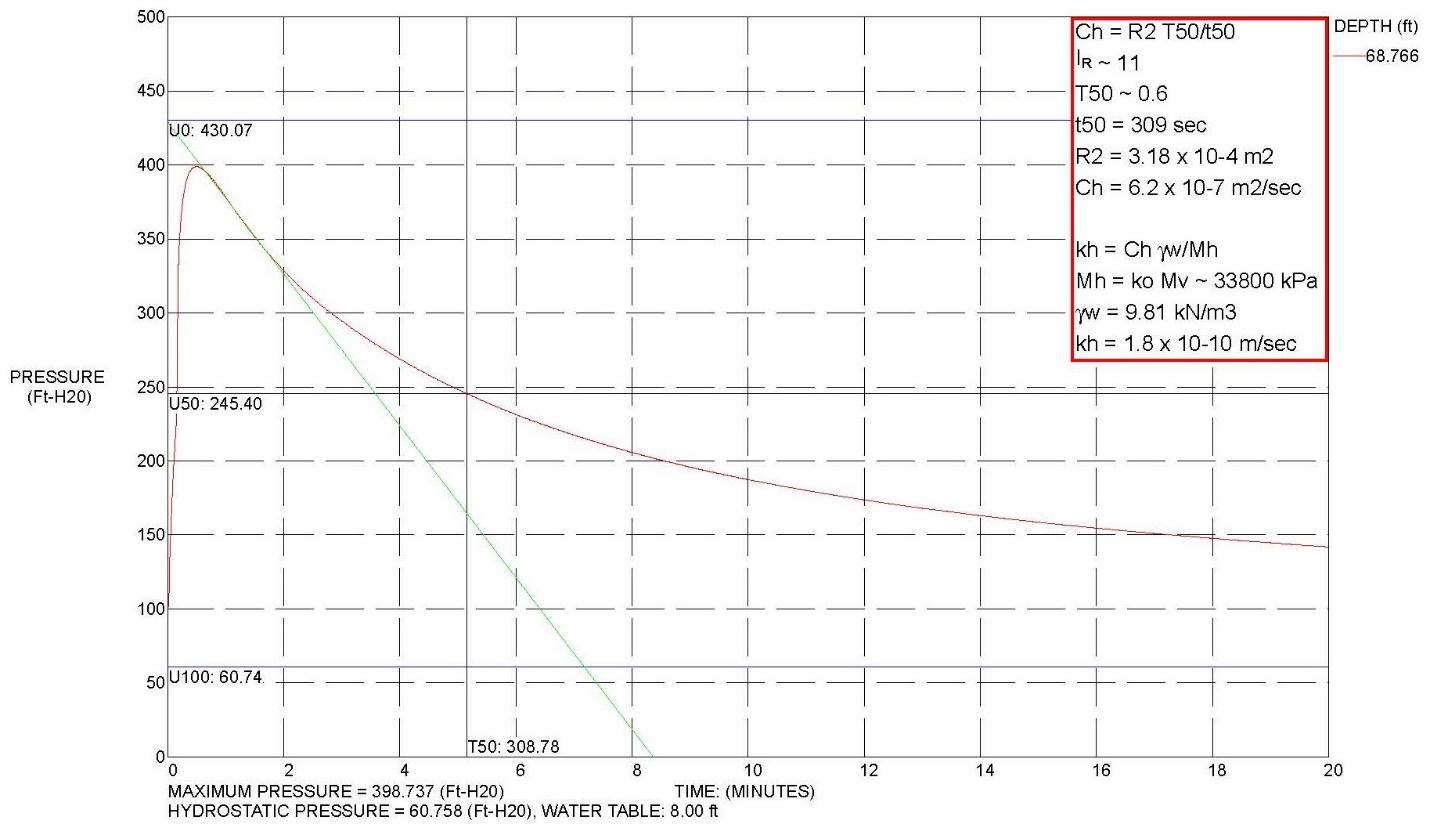In highly over-consolidated clays, the pore pressure initially increase before decreasing due to the redistribution of excess pore pressures around the tip before they reach an equilibrium state and radial drainage occurs. Figure 10a shows an example of a pore water pressure dissipation test for a normally consolidated clay and figure 10b presents an example of a dissipation for a highly over-consolidated clay.
Figure 10a: Example of processed dissipation test data for normally consolidated clay
Figure 10b: Example of processed dissipation test data for an over-consolidated clay
Figure 11 presents an example of corrected cone penetrometer test results. From the CPT data close depth interval measurements, they provide excellent resolution for soil stratigraphy. Because the engineer does not visually inspect a soil sample, he/she correlates, instead, the soil behavior type from the tip resistance, friction sleeve resistance and pore pressure. The soil behavior types accurately correlate from either 2 or 3 independent parameters. When the soil behavior types do not agree between the charts, the engineer should either review soil samples or perform pore pressure dissipation tests to determine which the classification chart best agrees. Any excess pore water pressures take longer to dissipate in cohesive soil than in cohesionless soil.
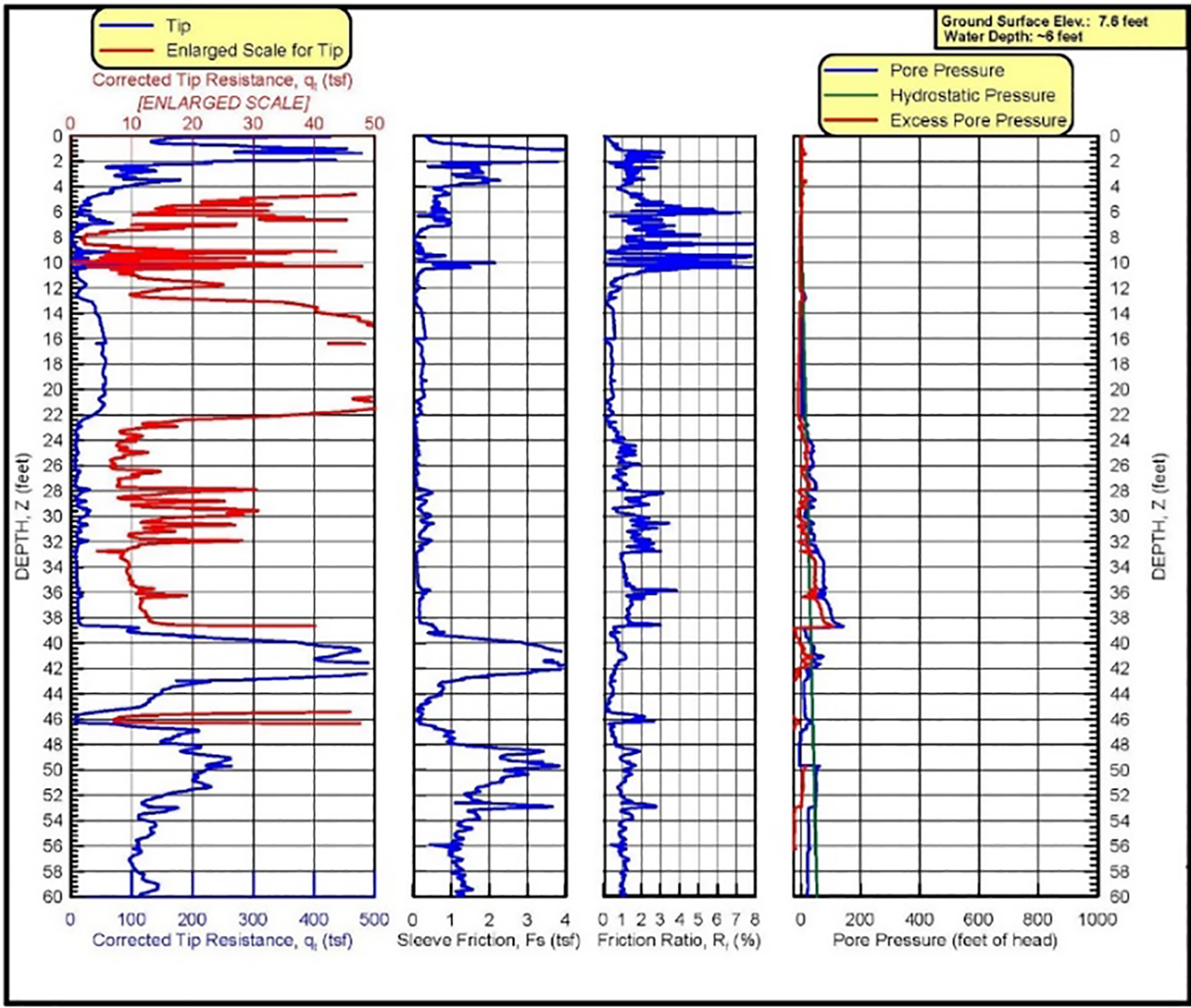
Figure 11: Example of corrected CPTU test results
Interpretation of CPTu Data
Soil Behavior Type: In 1986 Robertson and Campanella developed two separate soil behavior type charts: 1) tip resistance versus friction ratio, Fr, and 2) tip resistance versus pore pressure ratio, Bq (Figure 12a). Both charts have 12 soil behavior types. Below 30 meters (100 feet) the soil behavior type zones shift somewhat from the increase of the vertical stresses. Robertson (1990) updated the soil behavior type charts to normalize those axis accounting for the vertical stress (Figure 12b). However, unlike Robertson’s earlier soil behavior chart that had 12 zones for both the friction ratio and pore water pressure charts, the updated charts have 9 zones for the friction ratio and 7 zones for the pore water pressure charts. Both sets of charts have discrepancies where either the minimum or maximum tip values differ for the friction ratio or pore pressure charts as shown on the Table 1.
Table 1: Discrepancies in tip resistances for SBT charts
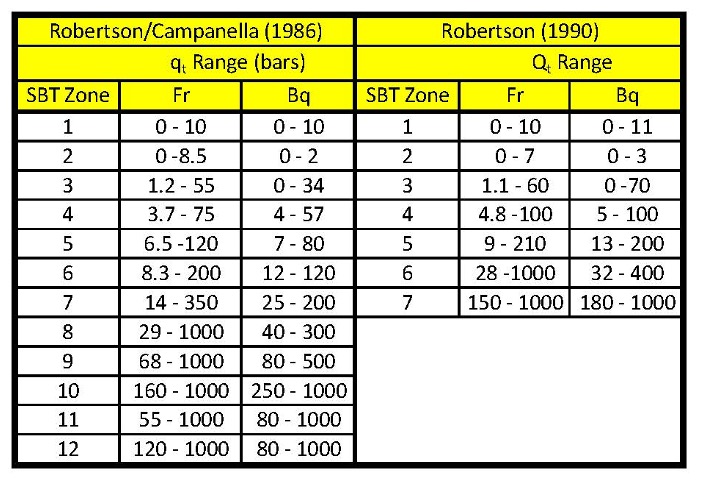
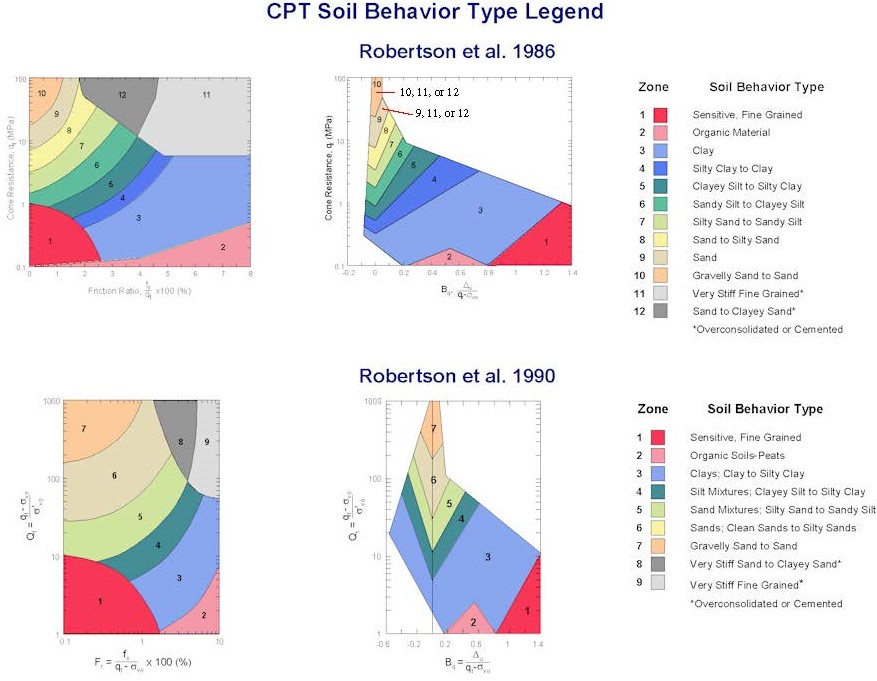
Figures 12a &b: Soil Behavior Type Correlation Charts
Jefferies and Davies (1991) developed a soil type classification system using the tip resistance, friction ratio and pore pressure ratio to calculate a material index, Ic, with following equation:
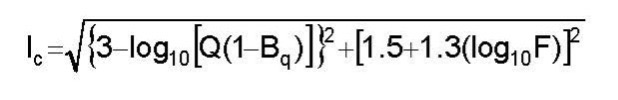
Where Ic < 1.8, the soil is cohesionless and where Ic > 2.76, the soil is cohesive. Concentric circles with their center at log10(Q(1-Bq)) = 3 and log10(F) = -1.5 define the soil behavior zones (Figure 13).
|
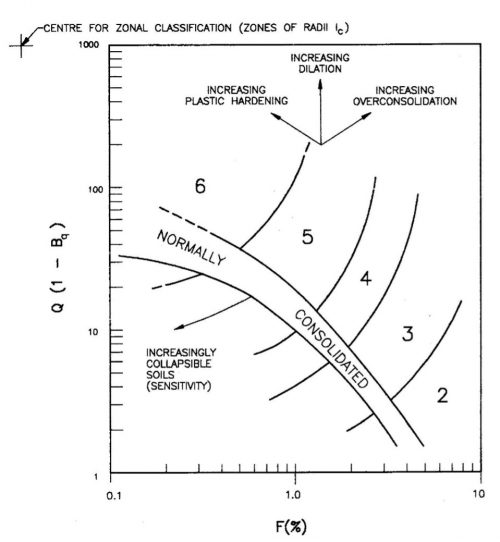
Soil Behavior Type from Ic |
||
| Ic | Zone | Soil Classification |
| Ic < 1.25 | 7 | Gravelly sands |
| 1.25<Ic<1.90 | 6 | Sands-clean sand to silty sand |
| 1.90<Ic<2.54 | 5 | Sand mixture-silty sand to sandy silt |
| 2.54<Ic<2.82 | 4 | Silt mixtures-clayey silt to silty clay |
| 2.82<Ic<3.22 | 3 | Clays |
| 3.22<Ic | 2 | Organic soil–peat |
| Q(1-Bq)<10 & F<1% | 1 | Sensitive fine grained soils |
Figure 13: Ic Soil Behavior Type Classification Chart
From grain size analyses at mine tailing sites, Jefferies (1993) developed the following correlation for fines content or the percentage passing the number 200 sieve as below based on Ic (Figure 14).
% Passing #200 = 42.4179*Ic-54.8574 For 1.2933 < Ic < 3.6508
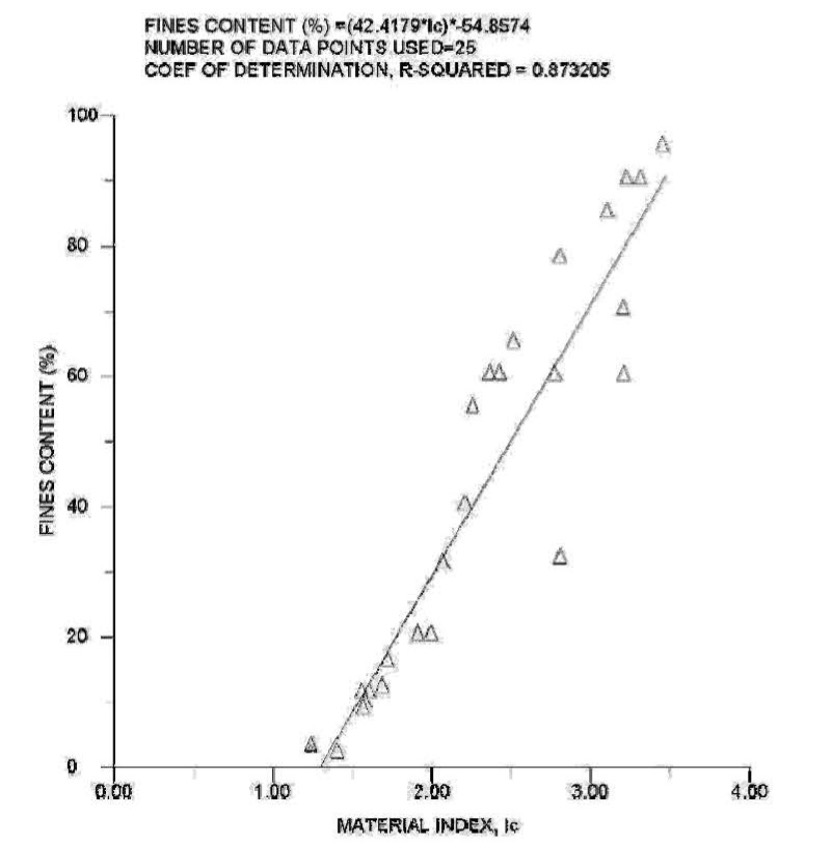
Figure 14: Estimating fines content from Ic
Figure 15 presents an example CPTU sounding showing its soil behavior type and fines content.
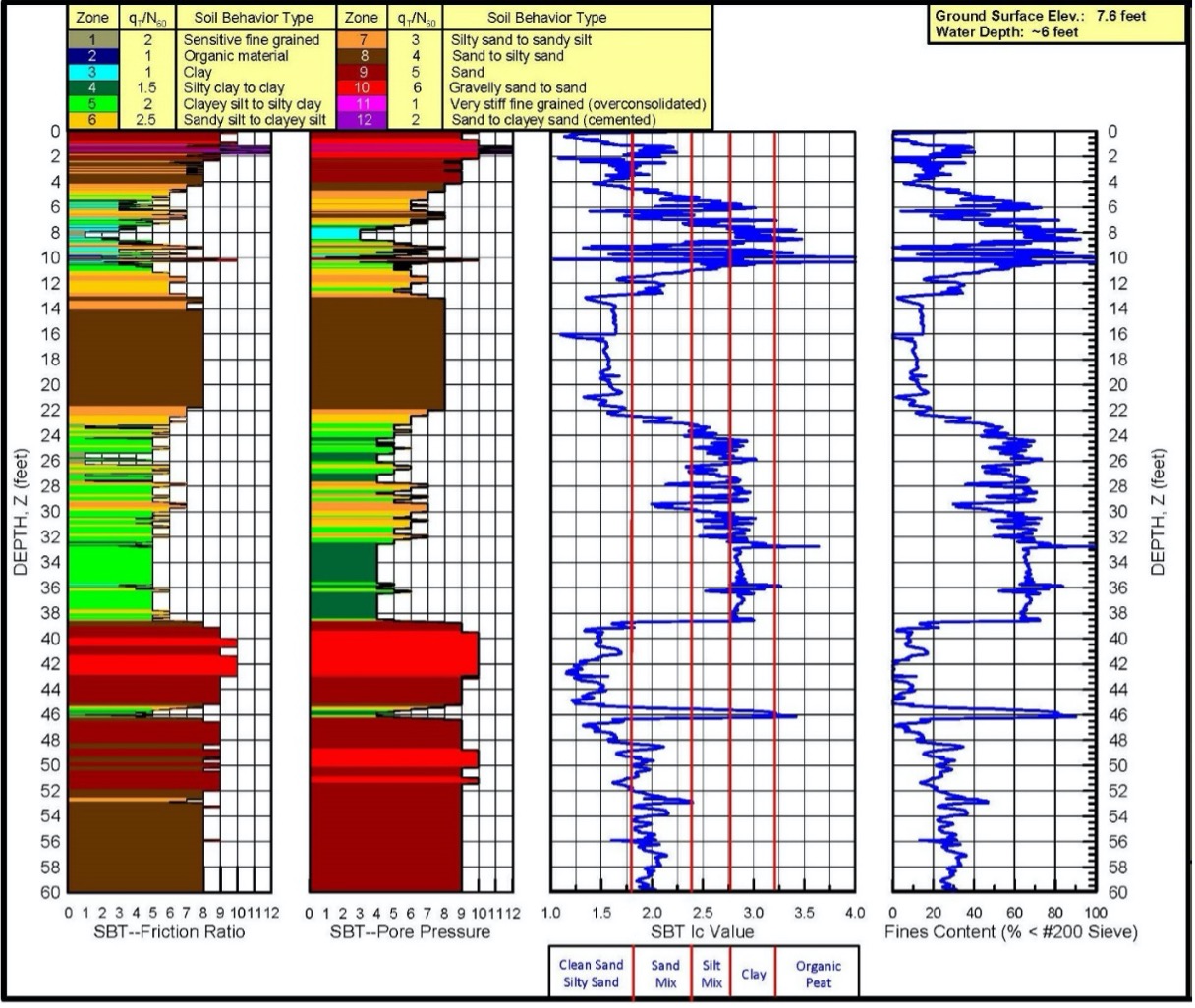
Figure 15: Example soil behavior type classification
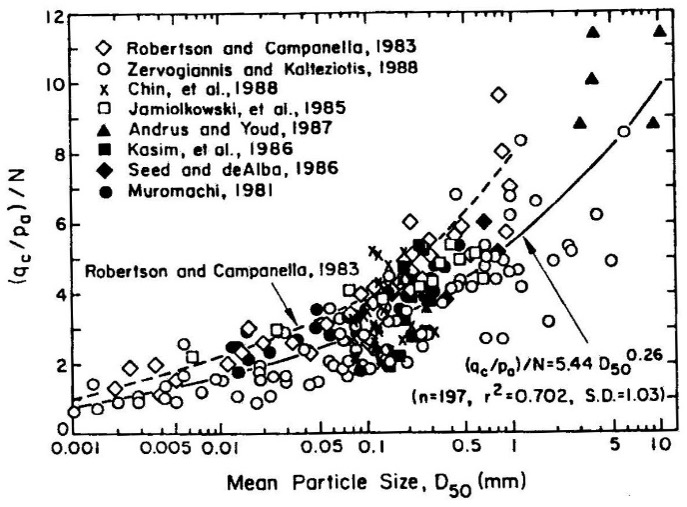
CPT-soil shear strength interpretation: Jefferies and Davies (1993) developed the following equation to compute SPT N60 values based on the Ic value and tip resistance (Figure 16):
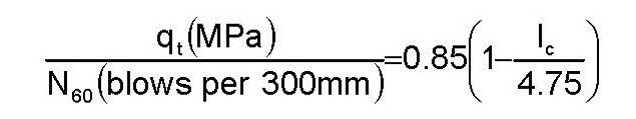
Figure 16: SPT/CPT correlation
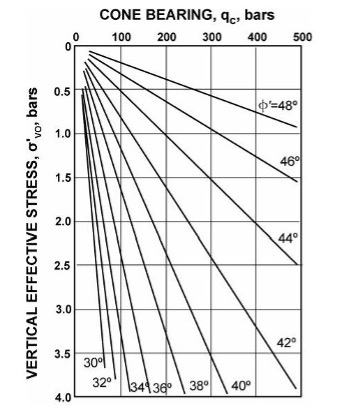
Where the soil behavior type value exceeds 5, the engineer may consider the soil to behave as a cohesionless soil and compute the angle of internal friction using either Robertson and Campanella (1983), Kulhawy and Mayne (1990), and Urielli et. al. (2013) methods (Figure 17a-c). For these methods, φ’ cannot exceed 50 degrees.
For Robertson and Campanella:
φ’ = tan-1((LOG10(qt/σv’)+0.29)/2.68)*180/π
For Kulhawy and Mayne:
φ’ = 17.6+11*LOG10[(qt/σatm)/sq. rt. (σv’/σatm)]
For Uzielli:
φ’ = 25.0o * [(qt/σatm)/sq. rt. (σv’/σatm)]0.10
Robertson and Campanella (1983)
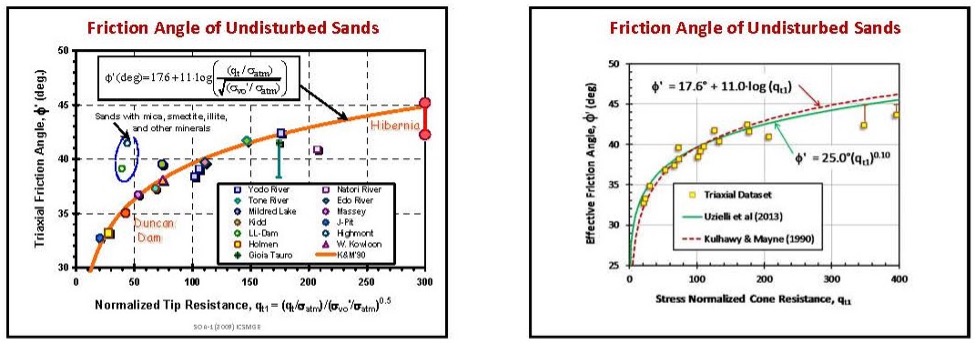
Figures 17 a-c: Correlations with angle of internal friction for cohesionless soil
Where the soil behavior type from the friction ratio chart is less than 7, the engineer can compute the undrained shear strength using the correlation formula below.
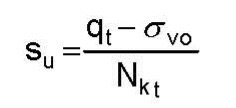
Where σvo equals the total overburden vertical stress and
Nkt is a correlation factor that ranges from 10 to 20 depending on the geology of the soil.
For sensitive soils, lower values of Nkt should be used.
Where the soil behavior type from the pore pressure ratio chart is less than 7, we compute the undrained shear strength using the correlation formula below.
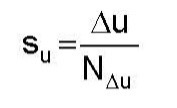
Where Du equal the excess pore water pressure and
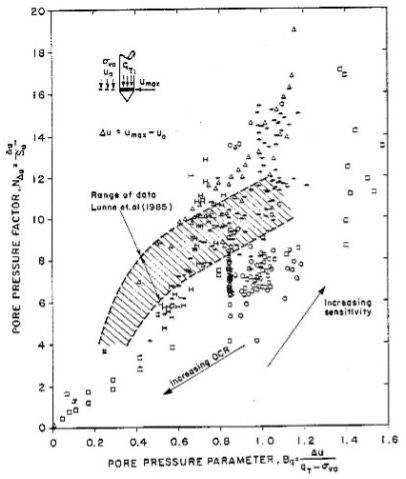
NΔu ranges between 2 and 20 (Figure 18).
Both undrained shear strength correlations use a single independent variable and have a wide range of correlation factors. Single variable correlations have low accuracies and need a second parameter or site-specific correlation to hone in on accurate shear strength predictions.
Figure 18: Wide range of NΔu
For cohesive soil, the following formula computes sensitivity shown below:
St = Su/Sremold = (qt– sv)/Nkt *(1/fs) = Ns/Fr
Ns = 15 for mechanical cones (Schmertmann 1978)
= 10 for electrical cones (Robertson and Campanella 1983)
= 7 for electrical cones (Robertson 2015)
= 6 for electrical cones (Greig 1985)
Figure 19 plots an example CPT sounding showing correlations for SPT N60 value, angle of internal friction for cohesionless soil, undrained shear strength for cohesive soil, and sensitivity for cohesive soil.
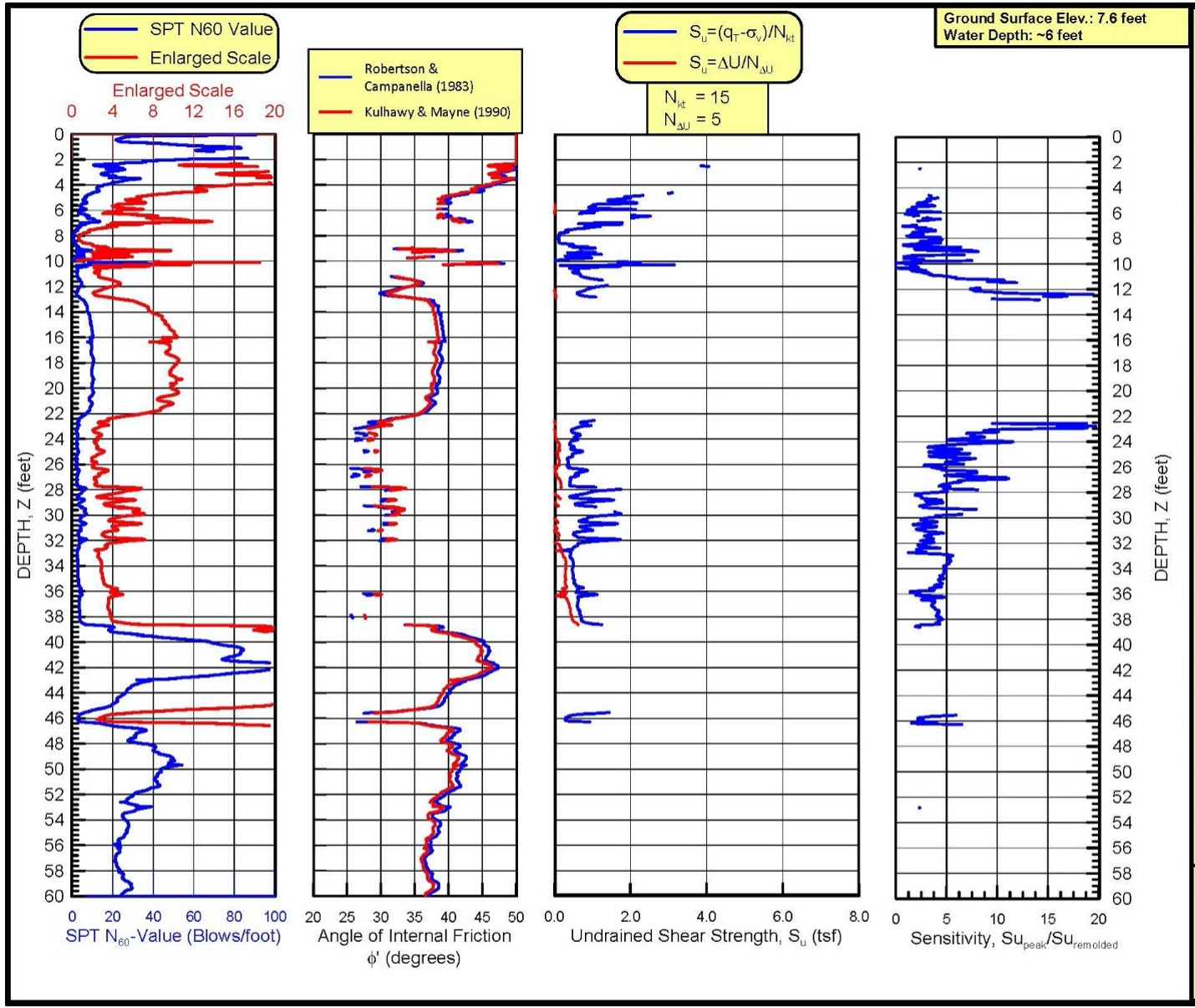
Figure 19: Example sounding showing shear strength correlations
CPT-soil modulus interpretation: Campanella (1998) estimates the over-consolidation ratio in cohesive soil using the following equation:
OCR = ((Su/σv’)/(0.11 + 0.0037 * PI))1.25
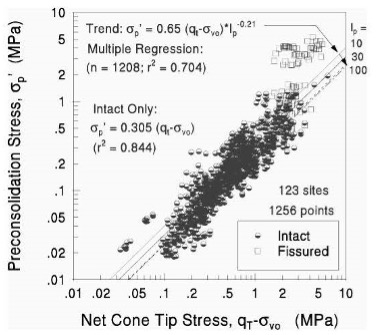
Lunne et al (1997) suggests computing the overconsolidation ratio using the following formula:
OCR = k * (qt – σv)/σv’
Where k varies from 0.2 to 0.5 with an average value of 0.3 (Figure 20 from Mayne).
Figure 20: Estimate of preconsolidation pressure in clay
This formula should only be used as a guide, as the CPT does not accurately measure stress history from a single variable correlation equation.
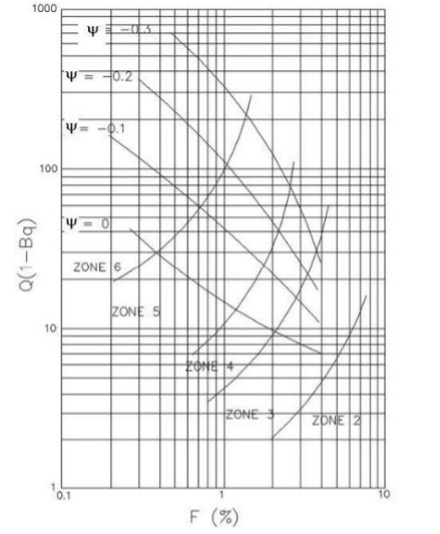
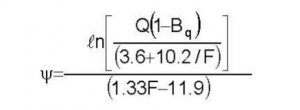
Plewes, et. al., 1992 estimates the state parameter with the below formula.
The state parameter plots on the Ic soil behavior type chart (Figure 21). Where the state parameter exceeds -0.1, soil may liquefy and these zones should be investigated more thoroughly.
Figure 21: State parameter plotted on Ic chart
The drained Young’s secant modulus at 25% failure stress has the formula, E25 = α * qt. The constrained deformation modulus also has a similar formula, M = α * qt. The engineer can choose α values and compute M. Because the E25 approximates 70% of M, he/she can compute E25 by multiplying the correlated M value by 0.70. The wide range of correlations for α values are shown below. Because the CPT deforms the soil quasi-statically instead of statically and strains the soil to failure, these single variable correlation predictions of deformation modulus have high uncertainty and error (Table 2a-b, Figure 22). Site specific correlations based on more accurate test data can significantly improve those correlations
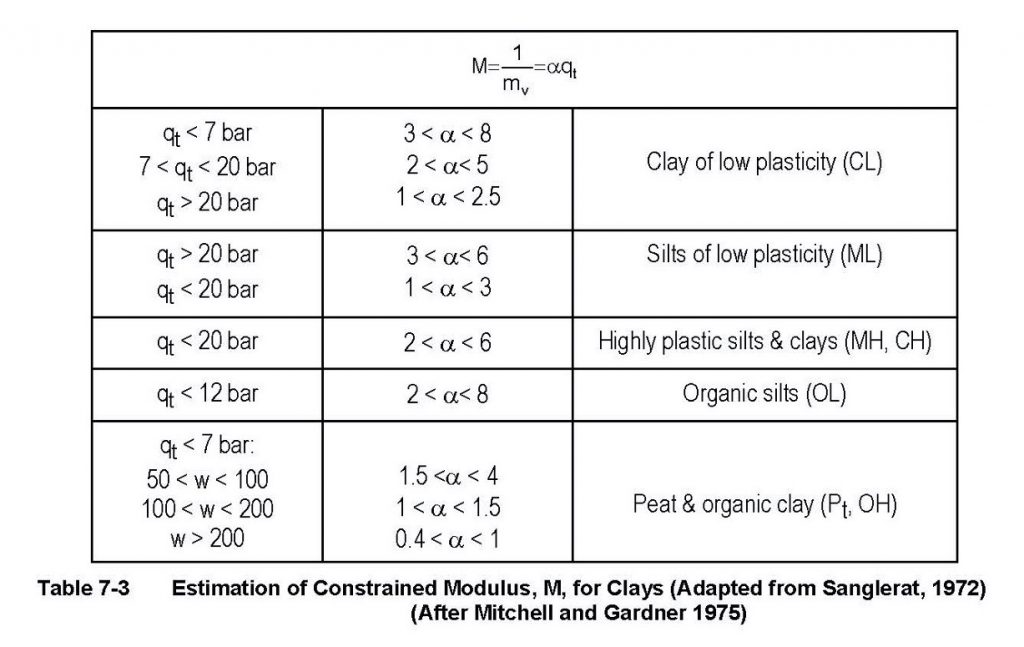
Table 2a: Range of α factors
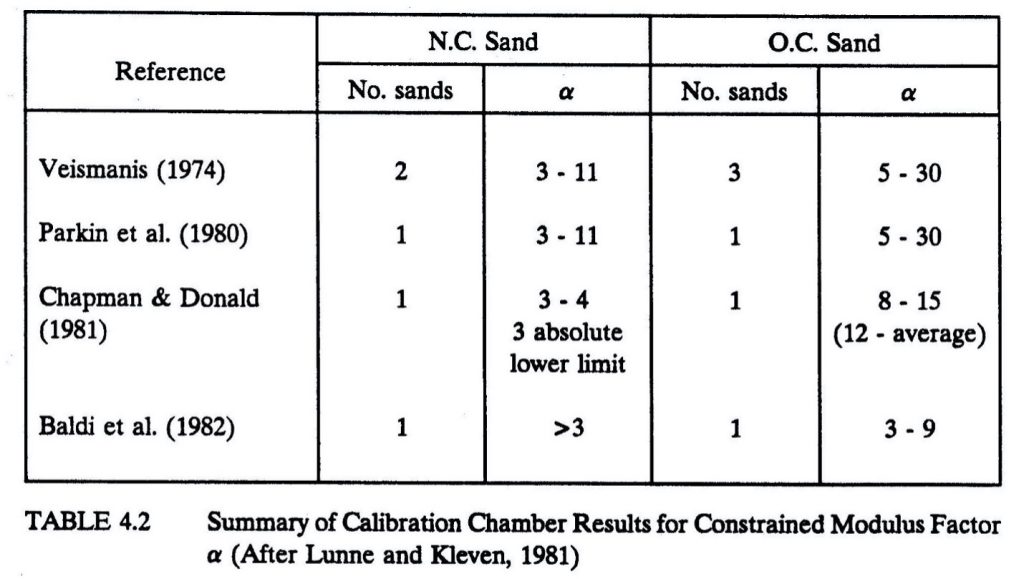
Table 2b: Range of α factors
Figure 23 shows an example CPT sounding for correlations of the over-consolidation ratio for cohesive soil, the state parameter, Ψ, the secant Young’s elastic modulus at 25%, and the constrained deformation modulus.
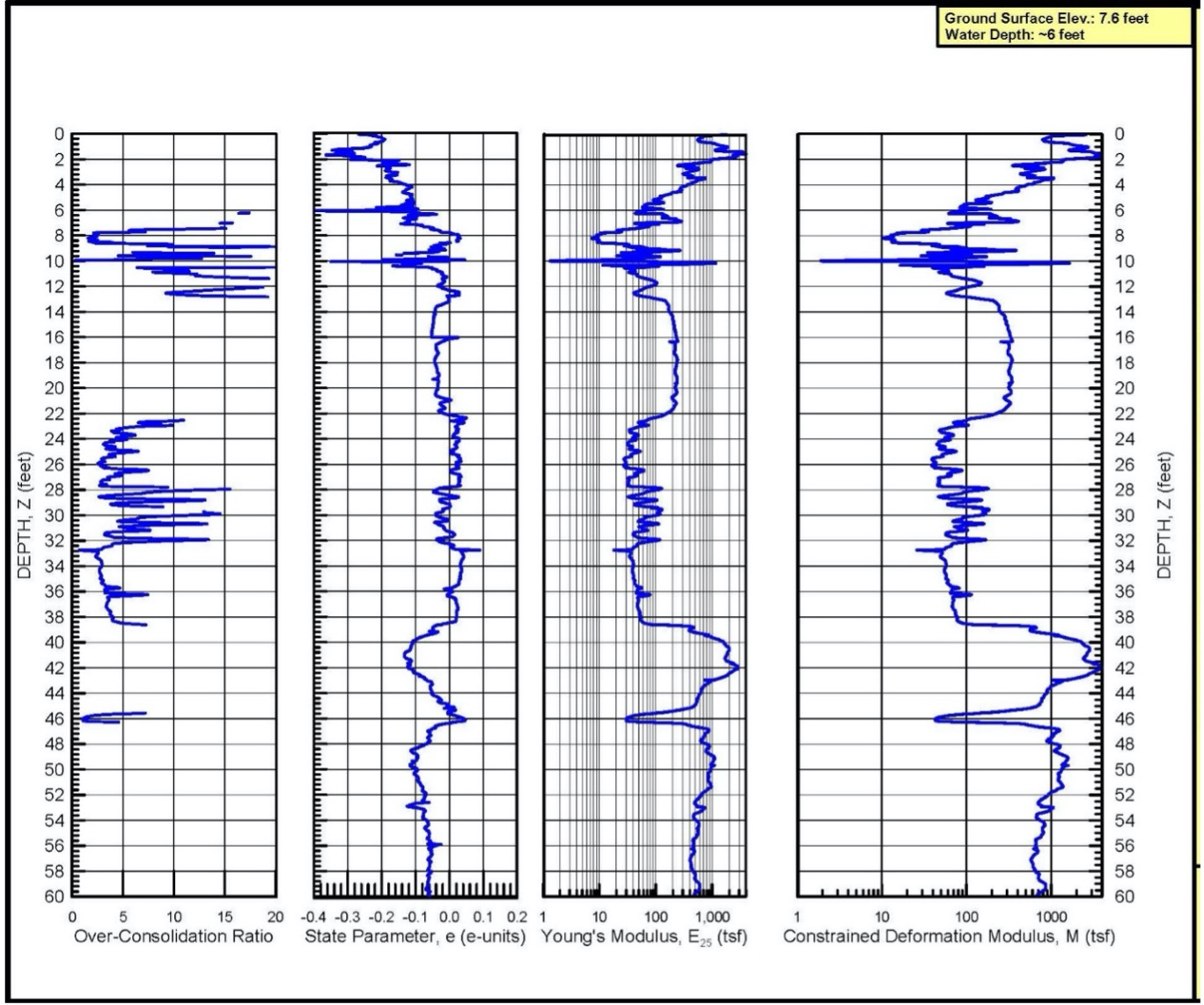
Figure 23: Example of CPT sounding showing stiffness properties
Vertical Pile Capacity
Engineers can accurately predict vertical pile capacity with CPT data (the cone models a pile). Robertson, Campanella, Davies, and Sy (1988) show that direct methods based on tip and friction sleeve resistances predict better than indirect measurement methods based on correlations with shear strength. The three most accurate methods are 1) Schmertmann and Nottingham (1978) — qc and fs used, 2) de Ruiter and Beringen (1979) — qc and fs used, and 3) Laboratoire Central des Ponts et Chaussées (1982) — qc only used. With these methods, their study showed that the predicted pile capacity for steel pipe piles averaged within 10% of the measured capacity with a standard deviation of less than 25%. Engineers should use caution when predicting pile capacities with CPT in cemented soils. The cone detects the cementation (high qc values), while pile driving may destroy the cementation. The LCPC method filters out data that are either 30% higher or lower than an average value within 1.5 of the pile diameter or width zone. The Schmertmann and Nottingham method also removes spikes in tip resistances and averages those zones with the analyses. All three methods compute the ultimate pile by summing the end bearing resistance and the frictional side resistance.
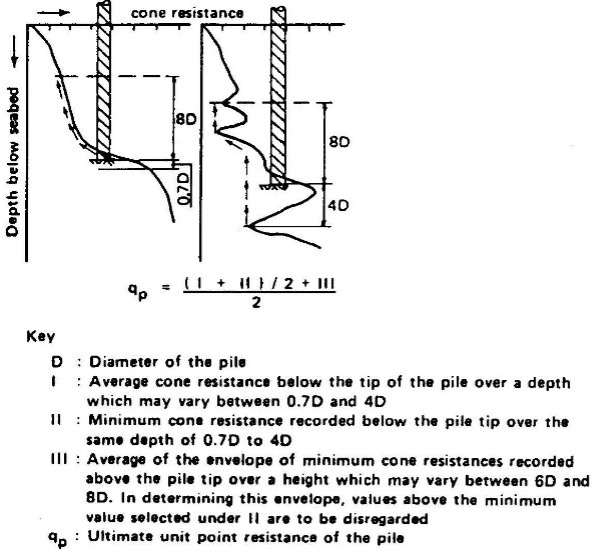
DeRuiter and Beringen method: The unit skin friction for sand equals the minimum of:
0.12 MPa,
CPT sleeve friction, or
qc/300 (compression):qc/400 (tension).
The unit end bearing in sand equals the minimum from Figures 24a-b.
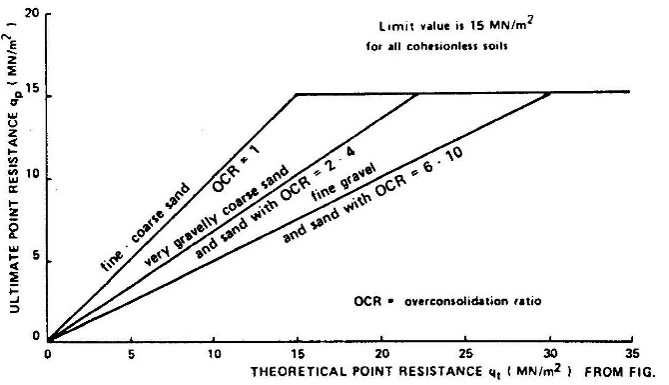
Figures 24a-b: Computing end bearing for piles using DeRuiter and Beringen method
The unit skin friction for clay equals a * Su, where a = 1 for normally consolidated clays or 0.5 for over-consolidated clays. The unit end bearing in clay = 9 * Su.
Schmertmann and Nottingham method: For the unit skin friction for sand the engineer uses his/her judgment to choose the most accurate value from the following (Figure 25a-c):
0.12 MPa,
K * fs for L > 8 * D {for L < 8 * D multiply by L/8D}, or
C * qc.
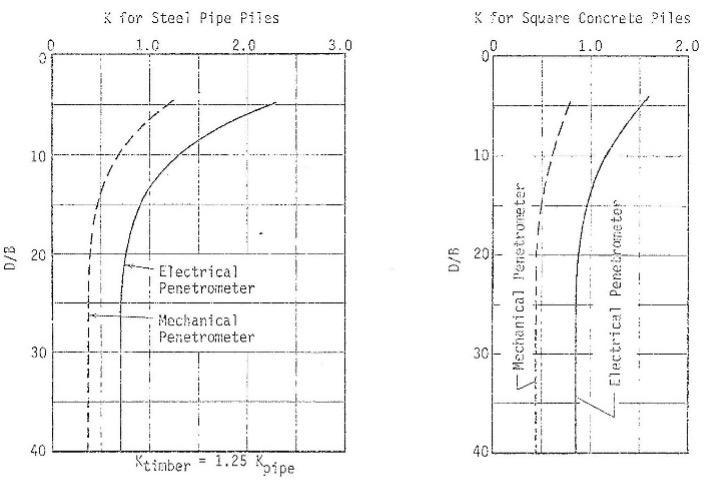
Figures a-c: Design coefficients for shaft friction of deep foundations in sand
End bearing for both cohesionless and cohesive soils use the method shown in Figure 26:
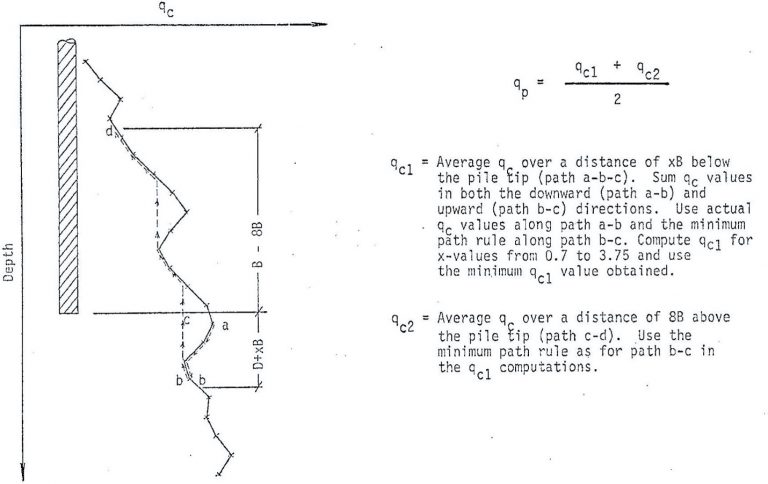
Figure 26: Method to calculate end bearing for Schmertmann and Nottingham method
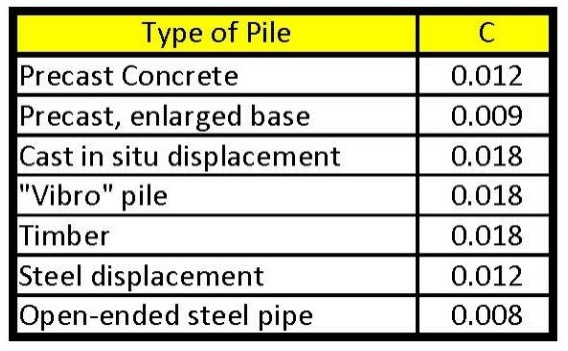
For cohesive soil the engineer calculates the unit skin friction from the following and chooses the most accurate value:
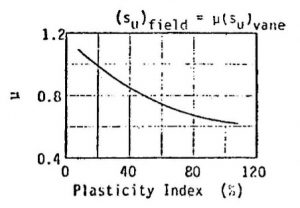
0.10* μ * qc(average) For electric cones (for mechanical cones multiply by 2/3), or
α’ * fs for L > 8 * D {for L < 8 * D multiply by L/8D}
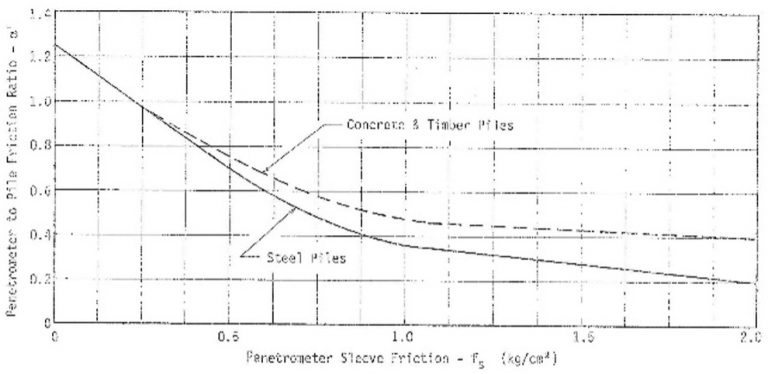
Figures 27a-b: Correlation coefficients to compute side resistance for cohesive soil
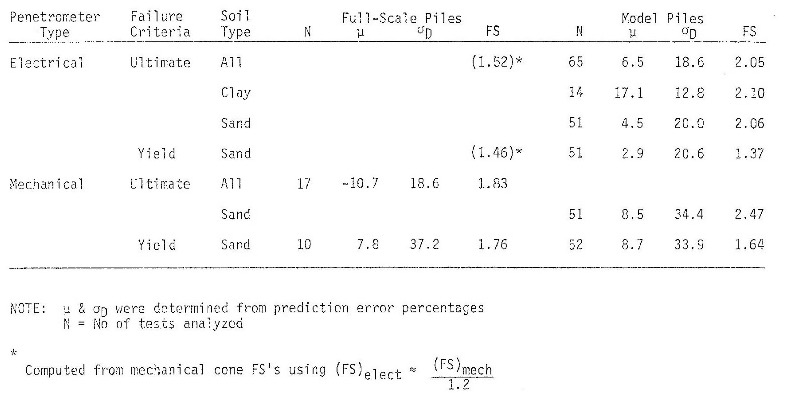
Nottingham shows the following accuracy for this method as Figure 28:
Figure 28: Accuracy of Schmertmann/Nottingham method
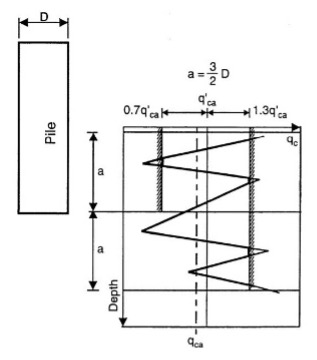For the LCPC method, the engineer clips the tip resistances that either exceed 1.3 times or less than 0.7 times the average tip resistance in the zone shown in Figure 29. He/she must use an convergence (via a do loop) process because the average value changes after each clipping iteration. The correlation factors depend on the soil type and deep foundation construction method as shown in Figure 30. An Excel spreadsheet that computes vertical pile capacity using the LCPC has the following link LCPC—the macro “qcaverage” clips the extreme values.
Figure 29: Clipping extreme values using LCPC
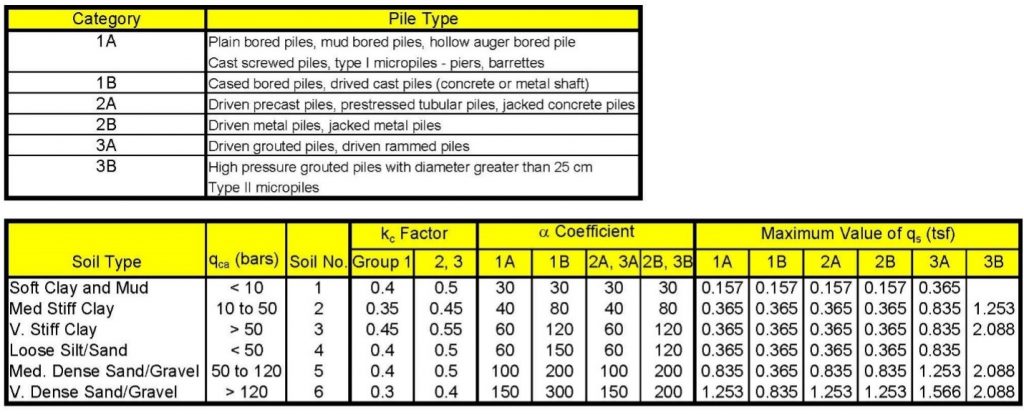
Figure 30: Correlation coefficients and maximum values for LCPC method
Figure 31 presents an example of vertical capacity of an 18 inch diameter auger cast pile based on the LCPC method.
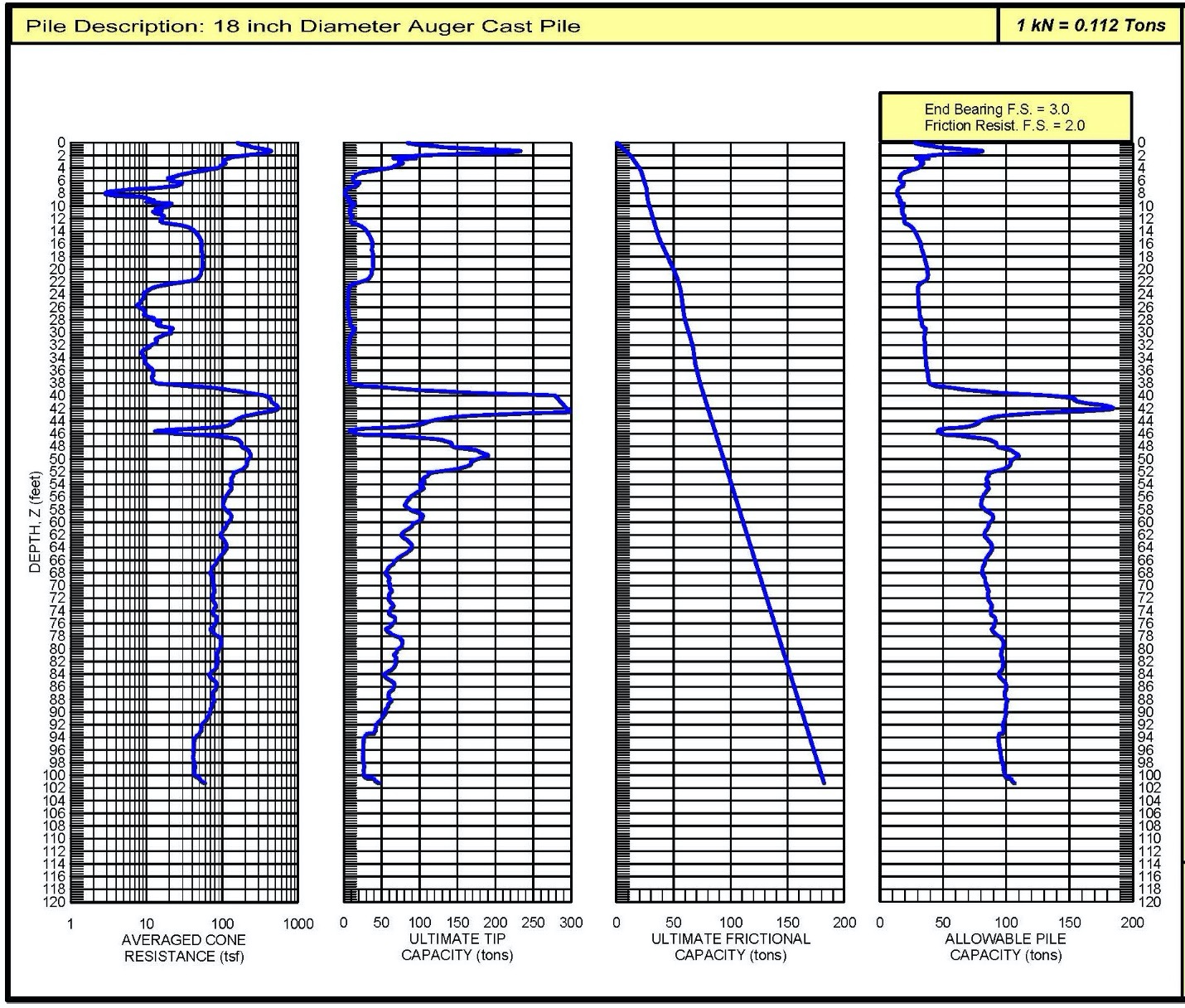
Figure 31: Example of LCPC calculation for vertical pile capacity
Wick drain design
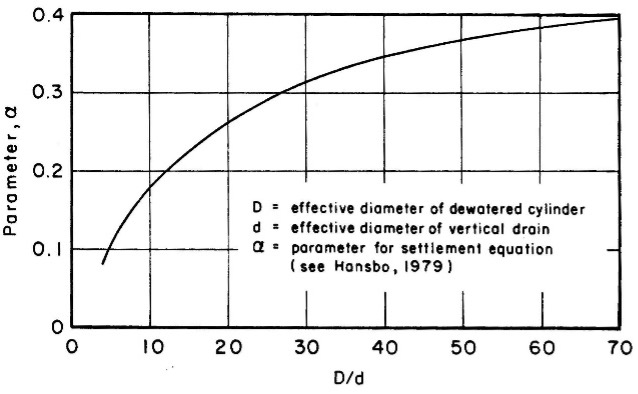
From dissipation test results, the engineer can compute the horizontal spacing for the desired consolidation time and percentage of consolidation using the following equation (Campanella 1998) [Figure 32a-c]. In Robertson/Campanella’s worked example, they found using a site-specific correlation for λ = 0.1 * Ch provided a better prediction than 0.5 * Ch.
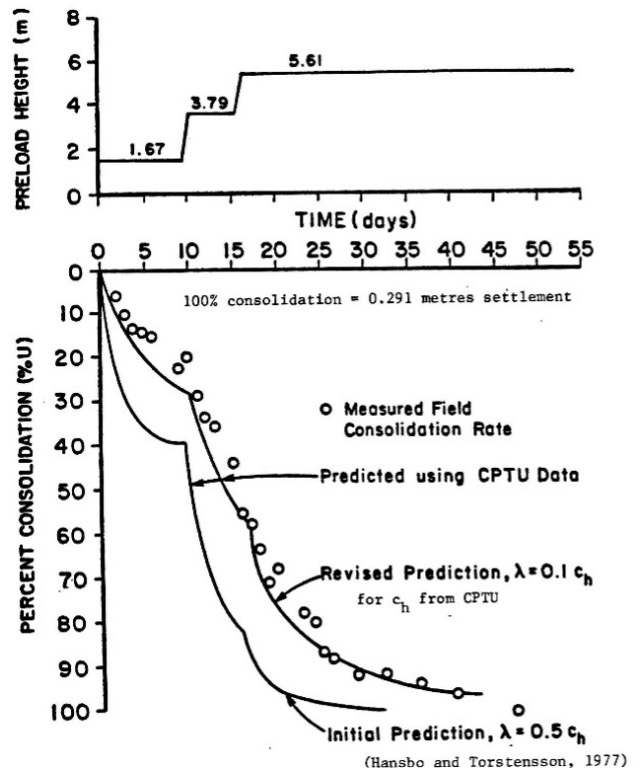
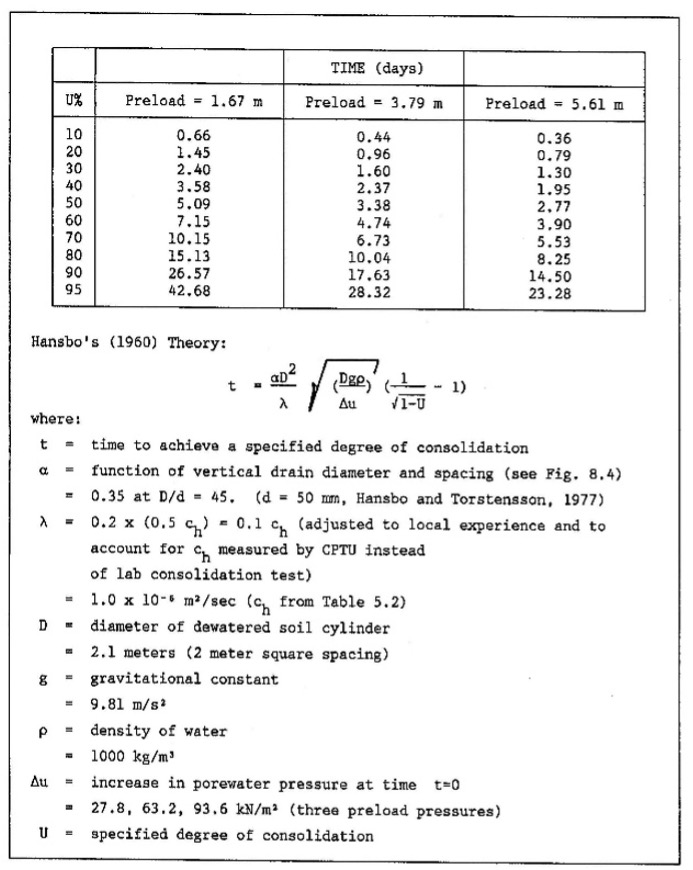
Figure 32a-c: Calculations for wick drain design from dissipation test
Settlement of Shallow Foundations
Schmertmann’s method (1970 & 1978) provides fair estimates of settlement for shallow foundations in normally consolidated or recently aged cohesionless soils. In over-consolidated sands the CPT tip resistance correlates with the constrained deformation modulus from a family of possible curves (Figure 33). Additionally, for cohesive soils, the CPT data have a wide range of correlation coefficients, a, and thus the engineer does not know which factor to use, resulting in inaccurate measurements of deformation moduli. The deformation correlation depends on a single variable, tip resistance, and not two independent variables to allow the engineer to hone in on the correct modulus. Thus, he/she needs information from other tests from the site to correctly select the correct curve from the family of curves and obtain the correct deformation modulus.
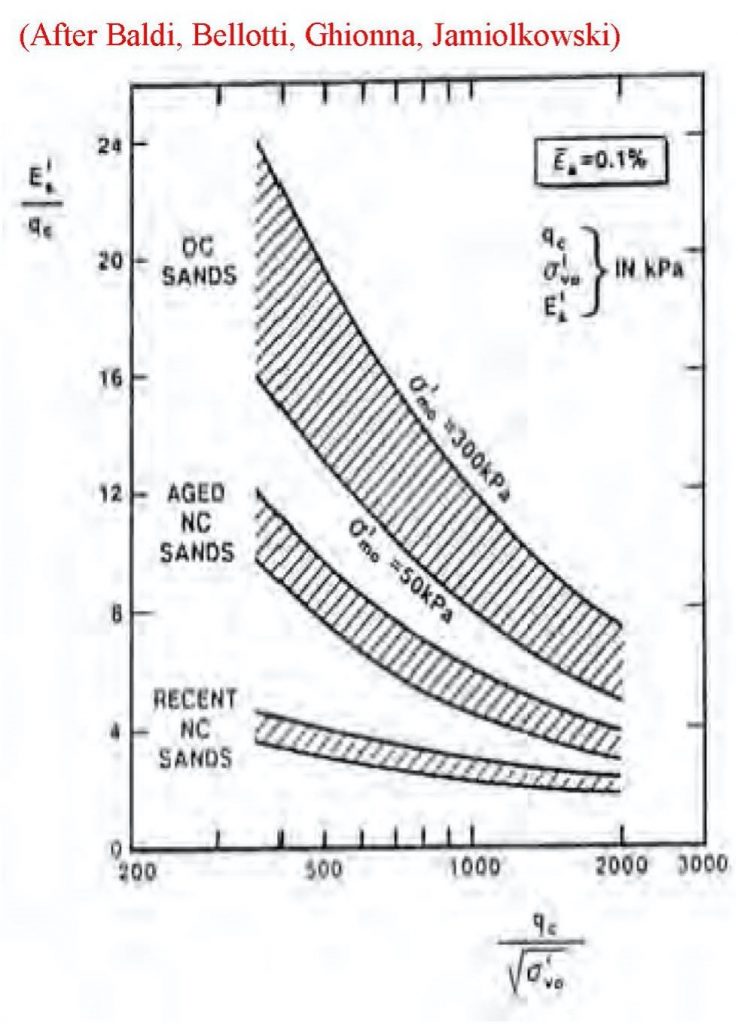
Figure 33: Wide range of family of curves for CPT tip resistance correlation factors and deformation modulus